Coase’s Theory of the Firm

During the Great Depression, British economist Ronald Coase wrote a famous essay on the nature of the firm or company. As with America at the time, many free-market economies were also enduring a severe and difficult economic depression. The Soviet Union, however, was growing to become a significant industrial economy. This led to a debate within economics on the merits of decentralized free-market economies that rely on prices to allocate goods and services versus centralized top-down planned economies.

Within the context of this debate, Coase observed that even free-market companies employ top-down planning. The key difference is that within free-market economies this planning and allocation take place within companies rather than governments. Free-market economies blend both planning within firms and decentralized production that is coordinated by prices within a marketplace.

If free markets and the price setting for goods and services within them are so efficient, as every free market economist since Adam Smith has articulated, then why do companies even exist? Couldn’t this within-company planning function be done more efficiently by the market? That’s a really good question!

Coase’s answer is not intuitive, but it is incredibly informative and explanatory about the socioeconomics of free-market societies. His answer is that companies exist, because of something called transaction costs.

What Are Transaction Costs?

Transaction costs are those costs paid during a transaction that do not flow from the buyer of a thing to the seller of a thing. They go somewhere else. Economists call these a wedge between the buyer and a seller.

Think about buying a house. There is some large amount of dollars during this transaction that will flow from the buyer to the seller of the house. Then there are also some not insignificant amount of dollars that will flow from either buyer or seller to third parties like real estate agents, a home inspector, a pest inspector, a radon inspector, a title insurance company, and so on. These costs are undeniably an inescapable part of the house buying transaction, but they are not part of the value that gets assigned to the house. They are transaction costs.

Transaction costs occur because the buyer cannot completely trust the seller. This lack of trust is usually a combination of a lack of complete trust in the seller’s transparency about the transaction and a lack of complete trust about the seller’s own knowledge about the transaction. So, the buyer and the seller use third parties to bridge this trust gap between them.

Why Companies Exist

Anyone who has ever bought a house knows that house-buying transactions are time-consuming and often difficult. These issues are magnified when you want to have somebody else perform a set of tasks for you, like developing artificial intelligence for your company, when you as a buyer aren’t able to completely specify what it is exactly that you want to be done.

If you can’t specify what you want that AI developer to do exactly, how can you write a legally enforceable contract to ensure that these things will be done? This issue is why it’s often easier to employ that AI developer under a simple labor contract instead of specifying all of those details in a freelancing contract.

The cost of that simple labor contract will be significantly smaller than the freelance one, because it will be simpler and standardized. This is much easier than trying to map out and plan every task in advance in such a way that it would be upheld in court.

As a consequence of this difference in contract costs, companies hire employees. As companies hire employees, companies of a nontrivial size emerge. This is all due to transaction costs between a buyer and a seller.

At their root, transaction costs are primarily due to a lack of social trust. If you knew and could trust that AI developer to do what would be best for your company, then you would probably worry less about specifying a contract that would hold up in court and may find it easier to allow that AI developer to freelance. This is also why word of mouth reviews of a company are so important to its ability to transact.

The Company Size Trade-Off

While we now understand why companies can be larger than a single person in terms of economic theory, we do not yet understand what determines the size of companies. Coase’s answer from his cool 1937 essay was that

a firm will tend to expand until the costs of organizing an extra transaction within the firm become equal to the costs of carrying out the same transaction by means of an exchange on the open market.

There are both internal and external costs to a company from getting something done that are in addition to paying for the actual labor itself. The external costs are transaction costs. Transaction costs increase the expense of operations between companies. The internal costs are management costs. Management costs increase the expense of operations within a company.

Management costs occur because big operations are increasingly costly to manage. That is, there are diminishing returns to management. Ask any manager and they will tell you that their job increasingly becomes managing people as the number of their direct reports increases instead of getting something operationally productive accomplished.

A good analogy for management costs is a pyramid. The more employees that are hired to bring tasks within a company, the more that the pyramid must expand. Labor costs for a company grow at a rate that is more than proportional to the range of tasks being performed. Management must ensure that its employees are accomplishing what they were hired to accomplish. This managerial overhead expense increases with each employee. In other words, management is similar to a transaction cost.

Therefore, there are diminishing returns to management. This makes in-house production inherently more expensive than the same production in the marketplace. In the absence of transaction costs, this economic relationship favors small companies over big companies. That is because small companies have a smaller managerial overhead burden than larger companies.

Mathematically Modeling Company Size

Coase was able to convey his brilliant theory of company size without really using any math at all. He used logic and plain English.

By converting Coase’s logical explanation into a model, we can further explore both supply chains and a common question confronting companies about whether to subcontract or outsource a task or to bring it in-house. In this simple model, I will consider a single product that is produced by a sequential chain of tasks.

These production stages are indexed by the variable t, which can range from 0 to 1 with 0 indicating no processing tasks have been completed and 1 indicating the product is finished.

Subcontracting

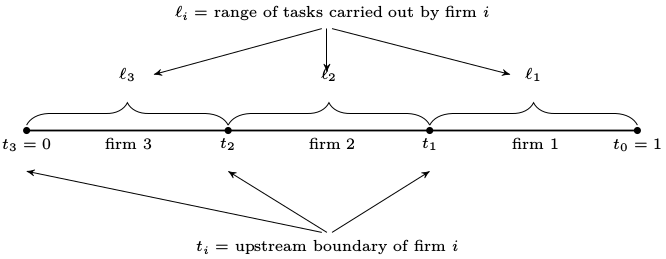
Each company within a value or supply chain chooses its upstream boundary. That is, it decides for itself what to process in-house and what to outsource. Its downstream boundary, its inputs, are taken as a given.

This implies that each company within the value chain faces essentially the same decision problem as the upstream firm above it in the value chain: How many processing stages should the company subcontract? The only salient difference is that each company’s decision space is a subinterval of the decision space of the company upstream of it.

Here’s a subcontracting example:

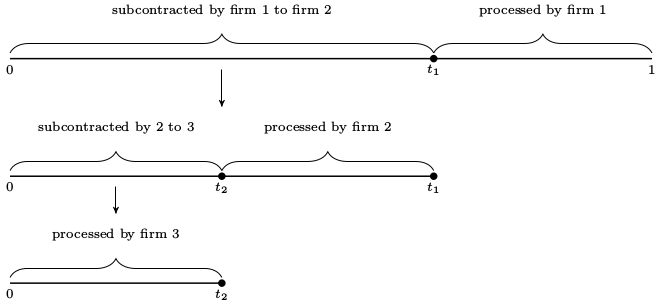
Firm 1 wants to sell 1 unit of a product to a buyer. It contracts with Firm 2 to purchase this partially finished product at stage t₁ so that it completes the stages from t₁ through stage 1 in-house.

Firm 2 repeats this procedure by contracting with Firm 3 to purchase the product at stage t₂. Firm 2 will then process the product from stage t₂ through stage t₁ in-house. Firm 3 processes the product from stage 0 through stage t₂.

Each company chooses its upstream boundary and treats its downstream boundary as a given. That is, Firm 1 purchases from Firm 2 and does not really care that Firm 2 subcontracted to Firm 3.

Costs

There are two types of costs as we consider company sizing. There are costs associated with diminishing returns to management. These are the rising costs per task incurred by a company when it expands the range of tasks coordinated by its managers. Let in-house tasks be denoted by ℓ and those costs denoted by c(ℓ) where c is increasing and convex. The average cost per task increases alongside the range of tasks that are performed in-house.

The other type of costs are transaction costs. In real life, transaction costs can be paid by the buyer, the seller or both of them. For ease of calculation, we can assume that the buyer pays for all transaction costs. This assumption does not meaningfully change anything, but it does simplify the math. So, for each transaction, the buyer pays more than the recognized face value of the product and the seller only receives the face value of the product.

Equilibrium

Assumptions

Let’s assume all companies in this supply chain are ex-ante identical price takers. They are all free to exit the market at their own choosing, and so there are never any negative profits. This means that all companies face the same price function p with p(t) meaning the price of the product at processing stage t. \[ \text{Function }p \text{ maps from } [0,1] \, to \, \mathbb{R_+}\]

Let’s additionally assume that there are no barriers to entry to this market. There can be a countable infinity of companies indexed by i that can enter and exit this market. This simplification means that there are no inherent advantages to incumbent companies within this value chain.

Informally, these result in an equilibrium that is an allocation of companies and a price function in which

1. Within this value chain, all active companies earn zero profit.
2. Within this value chain, no company has any incentive to deviate.
3. Within this value chain, there are no arbitrage opportunities available for an inactive company to enter the market and extract a positive profit.

Formally, an allocation of firms is a nonnegative sequence \[{\ell_i}\mathbb{i in N} \text{ such that } \ell_i = 0 \text{ for all sufficiently large } \mathbb{i}\]

A feasible allocation is one in which the entire production of the finished product is completed by a finite number of companies. \[\text{Given such a feasible allocation, } {\ell_i} \text{ let } {t_i} \text{represent the corresponding transaction exchange stages as defined by } t_0 = s \text{ and } t_i = t_i-1 – \ell_i\]

This price-allocation pair is an equilibrium for the value chain if:

1. \[p(0) = 0\]
2. \[pi_i = 0 \text{ for all }i \text{ and}\]
3. \[p(s) – c(s-t) – \delta p(t) \leq 0 \text{ for any pair }s , t \text{ with }0 \leq s \leq t \leq 1\]

Simulations

One of the primary benefits we derive from mathematical modeling is the ability to simulate what will happen when we adjust certain conditions or assumptions. These adjustments help to show us which features of our model have the most salient effects.

Transaction Costs Shape Markets

Within this value chain the number of companies active within it are determined endogenously by the primitives. That is, the value that we assign to transaction costs determines how many companies will enter and remain active within the value chain.

Transaction costs shape this value chain. As the value we assign to transaction costs increases, the number of companies that will be active within this value chain decreases.

When we set δ equal to 1.01, there are 64 companies within our value chain. When we increase δ to equal 1.05, the number of companies within our value chain declines to 41. When we further increase δ to 1.1, there will now only be 35 active companies within our value chain.

The takeaway is that higher transaction costs within a value chain will result in fewer companies operating within that value chain. Why does that matter beyond economic theory? Recall that the primary driver of transaction costs is a trust gap between buyer and seller. The bigger or more important that gap becomes, the higher transaction costs will be relative to the value of the product being exchanged. Thus, economic environments with relatively low social trust will have relatively higher transaction costs.

When companies are able to complete these value chain processing tasks in-house by managing employees at less expense than using subcontractors and paying for transaction costs, they will do so. These economic environments will then have relatively fewer companies within their value chains, because companies will internalize those transaction costs as management expenses. So, lower social trust implies fewer companies within a value chain, and by extension, within an economy.

A related implication of our model is that value added and company size increase at the downstream end of a value chain. Mathematically, this is due to the equilibrium price function being increasing and strictly convex. Intuitively, this means that for every company within the value chain, the marginal cost of their input from the company just upstream of itself increases as we move further downstream. That is, companies at the downstream end of a value chain choose to do more in-house than do upstream companies, and this choice makes them larger.

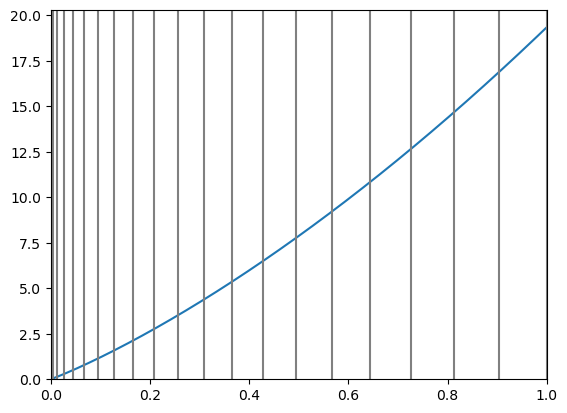
This graph depicts this price function. The horizontal axis from left to right is the stages along our value chain from the beginning raw material stage at point 0 to the finished product stage at point 1. The vertical axis reflects relative pricing of our product.

The takeaway from this is that transaction costs within a value chain force companies to be larger than they would otherwise be. Transaction costs prevent companies from mitigating against diminishing returns to management. In other words, a given company within a value chain would be more efficient if it had less management expense and could subcontract, but it can’t do that because the transaction costs from subcontracting are even more expensive than its own management expense. Mathematically, this relationship is reflected in the price function being convex.

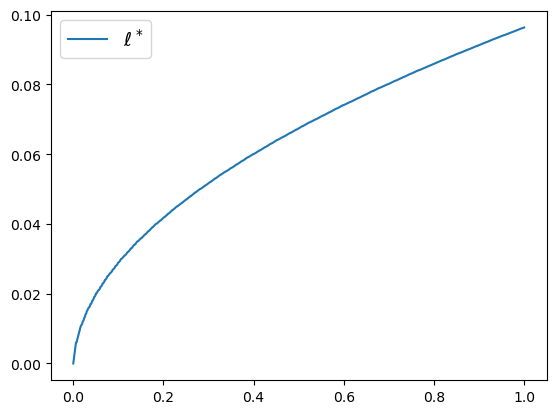
This graph depicts company size within our value chain. Along the horizontal axis from left to right is the value chain moving from raw materials at point 0 to our finished product at point 1. Along the vertical axis is company size from 0 to 0.1 relative to the size of the entire value chain.

Further, downstream companies within a value chain add more value and cost to the finished product relative to upstream companies. They have to in order to overcome their more significant internal management expense. This point may seem obvious and not worth mentioning, but it is very significant for strategic decision-making, especially for entities who are not producers along this value chain as well as for those who analyze the structures of economies and societies.

One implication is that large downstream companies cannot produce a finished product that costs less than an upstream company can. If you are an entrepreneur, an engineer, or simply a consumer and you want to use this value chain’s product in another value chain or for your own use, you should carefully consider whether or not you need the product in its final finished state or whether an intermediate state would also work.

Relatedly, not all value-adds by companies along a value chain are created equal. Remember that the finished product of this value chain was designed with an end-user or end-consumer in mind. You as a consumer, engineer or entrepreneur may not find all the value-adds as valuable as their ideal end-consumer does.

Secondly, and the model simplifies this away in its assumptions, but social power will coalesce around the larger companies at the downstream end of the value chain. Not only because of their sheer size but also because management and its managerial mindset inherently ameliorates transaction costs and the social conditions that primarily cause them. Their jobs also depend upon the existence of relatively high transaction costs and by implication relatively low social trust.